Trong một số dây chuyền cán thép sử dụng hai động cơ điện một chiều nối cứng trục người ta thường sử dụng một biến áp nguồn cung cấp cho mạch công suất điều khiển động cơ. Trong đó, biến áp nguồn có hai cuộn dây thứ cấp, một cuộn nối sao và một cuộn nối tam giác. Việc sử dụng biến áp nguồn như vậy cho phép triệt tiêu được một số điều hòa bậc cao ở phía sơ cấp.
Các nội dung được trình bày sau đây là dựa theo [1].
Sự dịch pha của các dòng điều hòa
Hình 1 là sơ đồ máy biến áp $\Delta/Y$ cung cấp cho một tải. Giải sử tỷ lệ điện áp $v_{AB}/v_{ab} = 1$ với tỷ lệ vòng dây là $N_{1}/N_{2} = \sqrt{2}$. Máy biến áp có góc lệch pha là $\delta = \angle \overline{v}_{ab} – \angle \overline{v}_{AB} = -30^{\circ}$.
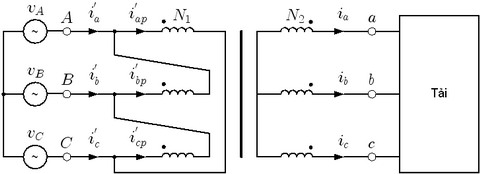
Với hệ thống 3 pha cân bằng, dòng điện dây của tải được biểu diễn như sa:
$$\begin{array} {rl} i_{a} &= \sum_{n=1,5,7,11,…}^{\infty} I_{n} sin (n\omega t) \nonumber \\ i_{b} &= \sum_{n=1,5,7,11,…}^{\infty} I_{n} sin (n(\omega t – 120^{\circ})) \label{EQ:DIGPIDEQ} \\ i_{a} &= \sum_{n=1,5,7,11,…}^{\infty} I_{n} sin (n(\omega t – 240^{\circ})) \end{array} $$
trong đó $I_{n}$ là giá trị đỉnh của dòng điều bậc $n$. Khi $i_{a}$ và $i_{b}$ được quy đổi về phía sơ cấp, các dòng điện quy đổi $i_{ap}^{‘}$ và $i_{bp}^{‘}$ được mô tả bởi
$$\begin{array} {rl} i_{ap}^{‘} &= i_{a} \frac{N_{2}}{N_{1}} = \frac{1}{\sqrt{3}} (I_{1} sin (\omega t) + I_{5} sin (5\omega t) + I_{7} sin (7\omega t) + I_{11} sin (11\omega t) + \cdots ) \nonumber \\ i_{bp}^{‘} &= i_{b} \frac{N_{2}}{N_{1}} = \frac{1}{\sqrt{3}} (I_{1} sin (\omega t – 120^{\circ}) + I_{5} sin (5\omega t – 240^{\circ}) + I_{7} sin (7\omega t – 120^{\circ}) \nonumber \\ & + I_{11} sin (11\omega t – 240^{\circ}) + \cdots \nonumber \end{array}$$
Khi đó dòng điện dây sơ cấp được tính như sau:
$$\begin{array} {rl} i_{a}^{‘} &= i_{ap}^{‘} – i_{bp}^{‘} = I_{1} sin (\omega t + 30^{\circ}) + I_{5} sin (5\omega t – 30^{\circ}) + I_{7} sin (7\omega t + 30^{\circ}) \nonumber \\ & + I_{11} sin (11\omega t – 30^{\circ}) + \cdots \nonumber \\ &= \sum_{n=1,7,13,…}^{\infty} I_{n} sin (n\omega t – \delta) + \sum_{n=5,11,17,…}^{\infty} I_{n} sin (n\omega t + \delta) \nonumber \end{array}$$
trong đó $n = 1, 7, 13, 19, \cdots$ là các thành phần thứ tự thuận, còn $n = 5, 11, 17, 23, \cdots$ là các thành phần thứ tự ngược. Như vậy, giữa dòng điện dây thứ cấp (dòng tải) và dòng điện quy đổi phía sơ cấp có góc lệch pha là
$$\begin{array} {rl} \angle i_{an}^{‘} &= \angle i_{an} – \delta \end{array} \qquad (1) $$
với $n = 1, 7, 13, 19, \cdots$ (các sóng thuận)
$$\begin{array} {rl} \angle i_{an}^{‘} &= \angle i_{an} + \delta \end{array} \qquad (2) $$
với $n = 5, 11, 17, 23, \cdots$ (các sóng ngược)
Triệt tiêu sóng hài
Để minh họa việc các dòng hài bị triệt tiêu bởi biến áp dịch pha ta hãy xét một ví dụ trên hình 2. Góc lệch pha giữa các cuộn dây thứ cấp đấu sao và tam giác là $0^{\circ}$ và $30^{\circ}$. Giả sử tỷ lệ điện áp là $v_{AB}/v_{ab} = v_{AB}/v_{\hat{a}\hat{b}} = 2$.
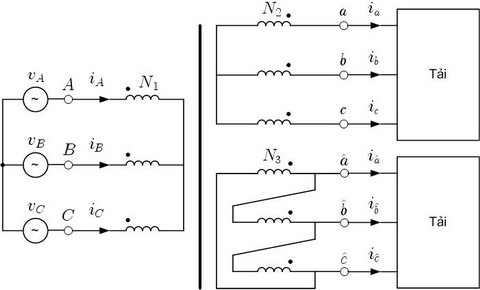
Các dòng điện dây thứ cấp được biểu diễn như sau
$$\begin{array} {rl} i_{a} &= \sum_{n=1,5,7,11,…}^{\infty} I_{n} sin (n\omega t) \\ i_{\hat{a}} &= \sum_{n=1,5,7,11,…}^{\infty} I_{n} sin (n(\omega t + \delta)) \end{array}$$
Do cuộn thứ cấp thứ nhất đấu $Y/Y$ nên khi quy đổi về phía sơ cấp thì góc pha của chúng không đổi, vậy nên
$$\begin{array} {rl} i_{a} &= \frac{1}{2} = (I_{1} sin (\omega t) + I_{5} sin (5\omega t) + I_{7} sin (7\omega t) + I_{11} sin (11\omega t) + \cdots ) \nonumber \end{array}$$
Để quy đổi$i_{\hat{a}}$ về phía sơ cấp ta lưu ý góc lệch pha của các thành phần thứ tự thuận và ngược theo công thức (1) và (2). Khi đó
$$\begin{array} {rl} i_{a}^{‘} &= \frac{1}{2}\left(\sum_{n=1,7,13,…}^{\infty} I_{n} sin (n(\omega t – \delta) – \delta) + \sum_{n=5,11,17,…}^{\infty} I_{n} sin (n(\omega t + \delta) + \delta) \right) \nonumber \\ &= \frac{1}{2}\left( I_{1} sin (\omega t) – I_{5} sin (5\omega t) – I_{7} sin (7\omega t) + I_{11} sin (11\omega t) + \cdots \right) \nonumber \end{array}$$
với $\delta = 30^{\circ}$. Dòng điện dây sơ cấp sẽ được tính như sau:
$$\begin{array} {rl} i_{A} &= i_{a}^{‘} + i_{\hat{a}}^{‘} = I_{1} sin (\omega t) + I_{11} sin (11\omega t) + I_{13} sin (13\omega t) + I_{23} sin (23\omega t) + \cdots \nonumber \end{array}$$
Tài liệu tham khảo:
[1] B. Wu. High-Power Converters and AC Drives. Wiley-IEEE Press, 2006.




